Vectors
By DarthVader
Date: 2022-10-19
Topic: 175 see comments
Post views: 913
Vectors
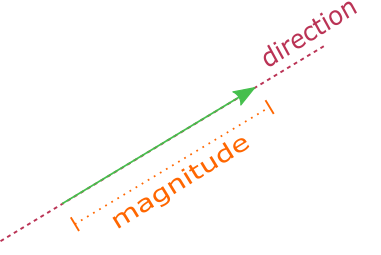
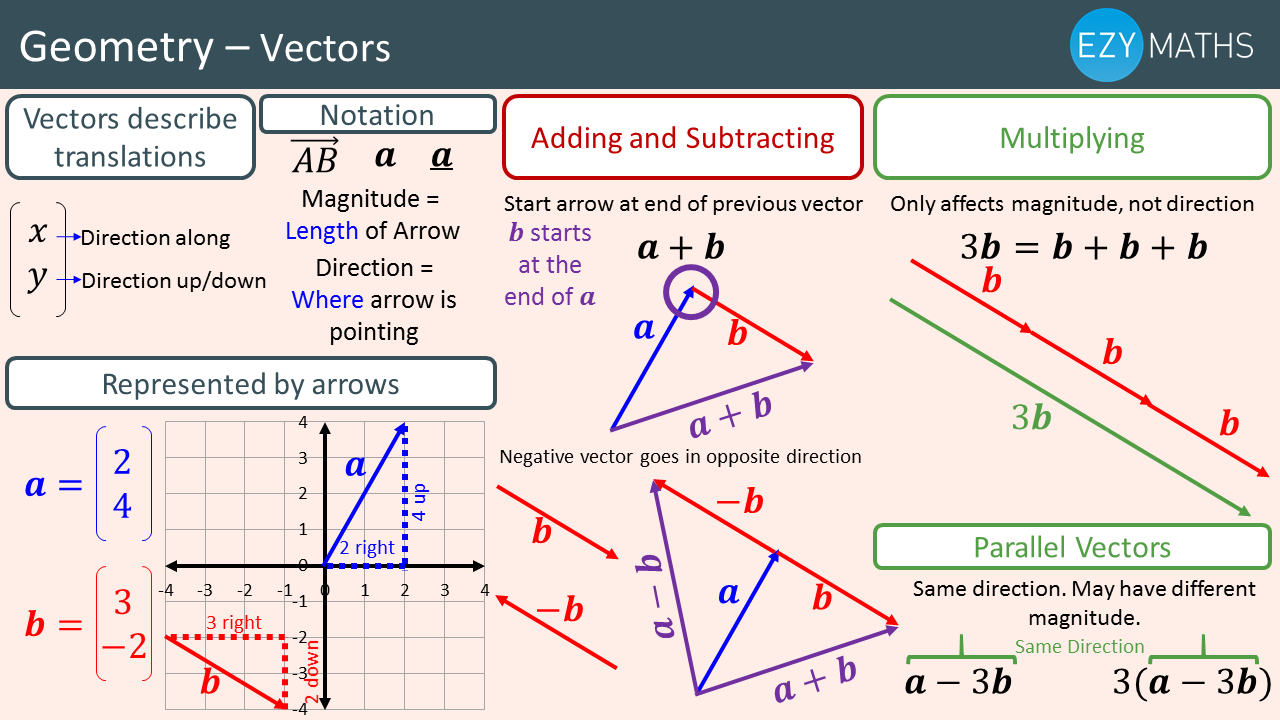
- A vector is a quantity that has both magnitude and direction.
It is useful to keep the idea of arrows in your head when thinking about vectors.
When trying to decide if a quantity is a vector or a scalar, it is useful to identify whether or not it makes sense to think of it as an arrow - is it acting in a specific direction?
Cartesian unit vectors:
Cartesian unit vectors are basically the x and y axis but specified as vectors.
- The x-axis is specified as the vector i
- The y-axis is specified as the vector j
In many free body diagrams it is useful to break up the vectors into i and j component vectors in order to solve problems.
Column form for component vectors:
The vector ai + bj can be written as:
[a/b]
(ai = horizontal component, aj = vertical component)
A vector written in this form is called a column vector.
Note: the / here is not a division sign but rather is only to indicate that a is place above b.
Resolving a vector into component form using angle θ:
If the vector v makes an angle θ with the positive x-axis, then:
v = (vcos θ)i + (vsin θ)j
where i is the horizontal component vector and j is the vertical component vector.
Magnitude and direction of a vector in terms of its components:
If vector v has the component form v = ai + bj, then its magnitude is given by:
v = √ a2 + b2
and its directio is given by the angle θ measured anticlockwise from the positive x-axis, where:
θ = tan-1(b/a)
Addition
Adding vectors in component form:
If a = a1i + a2j and b = b1i + b2j, then:
a + b = (a1 + b1)i + (a2 + b2)j
Scalar multiplication of a vector in component form:
If a = a1i + a2j and m is a scalar, then:
ma = ma1i + ma2j
Subtracting vectors in component form:
If a = a1i + a2j and b = b1i + b2j, then:
a − b = (a1 − b1)i + (a2 − b2)j
Properties of vector algebra:
- a + b = b + a
- (a + b) + c = a + (b + c)
- a + 0 = a
- a + (−a) = 0
- m(a + b) = ma + mb
- (m + n)a = ma + mb
- m(na) = = (mn)a
- 1a = a
Multiplication
Scalar product of vectors in terms of components:
If a = a1i + a2j and b = b1i + b2j, then:
a ⋅ b = a1b1 + a2b2
Scalar product of vectors in terms of magnitude and direction:
The scalar product of two vectors a and b is:
a ⋅ b = |a| |b| cos θ,
where θ is the angle between a and b.
Scalar product properties:
- If a and b are non-zero and perpendicular, then a ⋅ b = 0 and b ⋅ a = 0.
- a ⋅ a = |a|2
- a ⋅ b = b ⋅ a
- a ⋅ (b + c) = a ⋅ b + a ⋅ c
- (ma) ⋅ b = m(a ⋅ b) = a ⋅ (mb)
Finding the angle between two vectors:
The angle θ between any two non-zero vectors a and b is given by:
cos θ = ( a ⋅ b ) / ( |a| |b| )
Position vectors:
O⇢P
where:
O = the origin point
P = a point
and:
O⇢P = the total displacement from the origin to the point P. This is answered in terms of the component vectors i, and j, which are the horizontal and vertical components. This is basically x, and y, thus using cartesian coordinates.
Vector notation:
- Bold letters:
x - represents a scalar.
x - represents a vector.
- Underlining:
a - represents a scalar.
a - represents a vector.
- Arrows:
A⇢B - represents a vector where A and B are the start and end points.
Vector Equality
Two vectors are equal if their directions and magnitudes are equal.
Resolving Vectors
To calculate the resultant vector of a system of forces, first resolve each vector into its horizontal and vertical components. Then add up all the horizontal and vertical vectors, and calculate the resultant vector.
Up is positive, down is negative, right is positive and left is negative.
| Comments | Creator | Date | ID |
|---|